√無料でダウンロード! 理想気体 等温膨張 仕事 790620-理想気体 等温膨張 仕事
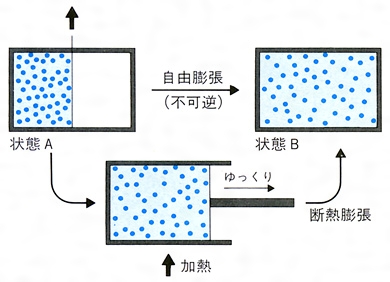
過程1;理想気体の準静的等温膨張過程なので,機関が持つ内部エネルギーの変化はない.熱力学第1法則より,高温 熱源(外部)から熱機関に入る熱qhと熱機関が外部にする仕事w'a→bは等しい.ここで,熱qhと仕事w'a→b は ともに正となる. w'a→b=qh (531)物理化学です。 150molの理想気体が300Kで0atmから最終圧力まで等温膨張により、365Jの仕事をした。 外圧が100atmとしたときの気体の最終圧力を求めよ。 どの公式を使って解けばいいのかわかりません。解き方を教えて下さい。 自由膨張とは,作業物質が系外に仕事を行わない膨張を指す。 例えば容積が固定された真空容器中への気体の膨張を考えればよい。 (下図参照) エントロピー増大の原理を前提とすれば,孤立系 (Δ U =0)としての断熱自由膨張は,温度変化がない理想気体に
準静的操作 等温操作
理想気体 等温膨張 仕事
理想気体 等温膨張 仕事- 理想気体を作業物質とし、温度 T h と T l で等温膨張、圧縮を行い、その間を断熱膨張、圧縮で結ぶ一連の反応をカルノーサイクルという。 1→2 等温可逆膨張 体積が V 1 → V 2 へと準静的に膨張する。 このとき、温度を一定に保つためには、高温熱源 T h41 理想気体への第1法則の適用 7 j i $ äa V V !




熱力学解説送ってくれると嬉しいです Clearnote
⚫ゆっくりと断熱膨張 断熱台 理想 気体 C B UEC The University of ElectroCommunications Department of Mechanical Engineering & Intelligent Systems 21 カルノーサイクル(3) 3等温圧縮(C→D) 3 4 3 log V V Q L W RT L ① 低温熱源に熱Q Lを放出, ② 等温圧縮. ③ 外部から仕事W 3V A B T ! 理想気体がする仕事(断熱変化) みなさん、勉強おつかれさまです!! 前回の単元では、「等温変化で理想気体がする仕事」について 学びましたね!! 1理想気体がする仕事 さて、今回もまずは復習です!! いままで、何回も出てきましたが、 「理想
作業物質として使う循環過程の熱機関(heat engine) を考える. 理想気体を作業物質と して使う循環過程の熱機関を考える. V P 1 2 4 3 I II III IV Figure 2 理想気体のカルノー・サイクル.I) 等温膨張,II)断熱膨張,III)等温圧縮,IV) 断熱圧縮. 1 (T h,V1,P1) −→ (T膨張した。このときのΔU、ΔH、q、wを求めよ。 変化 また可 = -1344 J = -228 kJ 4 1 mol の理想気体の系に、等温的に外界から1 の圧縮仕事 さ 解 は内部エネルギー変 が ΔU = したがって、 5 1 molの理想気体が300 Kで等温的に、7dm3から12 dm 解 等温 であるから、 等温変化とは, 気体の温度を一定にしたまま圧力や体積を変化させること です。 温度が一定ということは であるため,単原子分子理想気体のとき となります。 温度が変化しないため内部エネルギーも変化しない のです。 単原子分子理想気体ではなく
理想気体の等温変化を表すp-V曲線は右図赤線のような直角双曲線になります。 この曲線を特に等温曲線と言います。体積と圧力が と変化するとき、気体のした仕事Wは右図のp-V曲線とV軸,直線 , で囲まれる部分(右図黄色部分)の面積になります。 定積分によりWを求めると、絶対温度がTで7 実在気体の等温可逆膨張 ファンデルワールス気体において、温度と体積が (T, V i の状態から(T, V f) の状態へ、外圧と等しい 圧力を保ったまま等温可逆膨張したとする。ここで T、V i、V f が与えられたとき、気体が受け取る熱q と 仕事 w を求めよう。等温断熱自由膨張は,熱の出入りなしで,外部に仕事をしないで膨張する現象で,温度の変化が無いので,等温自由膨張ともいわれる。 体積 V の理想気体が真空に向かっていっきに 体積 V'まで 膨張 する場合,途中の温度を定義するのが困難であるが,変化の



熱機関の効率 ガス動力サイクル



Iwafunelab Iis U Tokyo Ac Jp
理想気体と過程に関わる公式集 Tweet 系がした仕事 を W ′ とおく。 系Aがそれぞれの過程を経て系Bに至ったとき、次の式が成り立つ。 ・定圧過程 一般的な気体 W A → B ′ = p ( V B − V A) 理想気体 W A → B ′ = n R ( T B − T A) ・等温過程 理想気体 W A → B(1) 等温膨張過程:高温熱源 t 1 か ら熱量 q 1 をシリンダー内に取り入 れながら 等温線 t 1 に沿って膨張し ながら外部に仕事をする。 (2) 断熱膨張過程:断熱線に沿って 低温熱源の温度 t 2 に達するまで膨 張しながら外部に仕事をする。 (3) 等温圧縮過程(等温変化における理想気体のする仕事と気体が吸収する熱量)equitempqatex 1 nmol(モル)の理想気体が、温度T を一定に保って、体積V1 からV2 まで準静的に変化 したとき、系(気体)が外界にする仕事W を求めよ。 ただし、ガス定数をRとせよ。 2
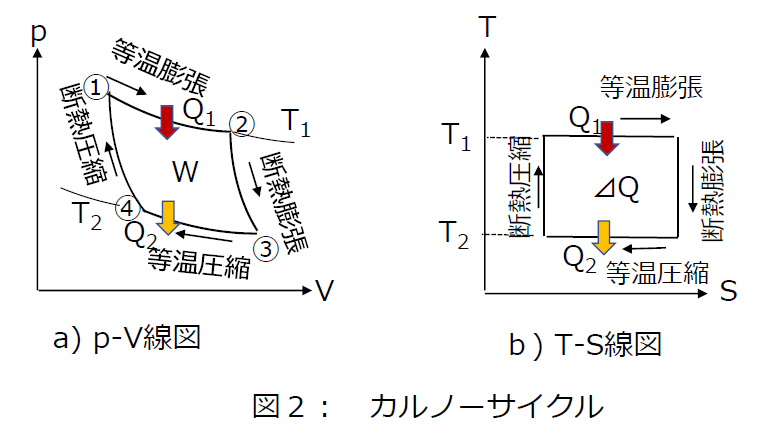



機械設計マスターへの道 カルノーサイクルと逆カルノーサイクル 熱力学の基礎知識 アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション




等温変化における仕事の求め方と圧力との関係 例題付き
26 理想気体の断熱変化(断熱膨張) ・(基本2) 断熱膨張で,系が仕事をする場合,系はその内部エネルギーを放出す るので,系の温度は下がる。(断熱圧縮では,逆に温度は上がる) W=ΔU=U 2−U 1=dU U 1 ∫U 2=nC V,mdT T 1 T 2=nC V,m(T 2−T 1)=nC V,mΔT理想気体温度計:理想気体では、圧力p、体積V、モル数n、気体定数R (= 1 J/K mol)、 温度T として、ボイルシャルルの法則pV = nRT が成り立つ。一定圧力下における膨張を温度計とみなす ことができる。 ¥ 演習問題#55-1(3)逆等温「圧縮」と可逆断熱膨張とを組み合わせた以下の操作(32B)を行えばよい。 ただし,大きく膨張できる状態は気体に限られる。 30)理想気体では (𝜕 ∂ ) =0なので,可逆等温膨張で∆ =0となり,𝑄a= =𝑄bとなる。



物理学の問題です わかる方よろしくお願い致します ある気体を図に示 Yahoo 知恵袋



理想気体の性質と状態変化 数学活用大事典
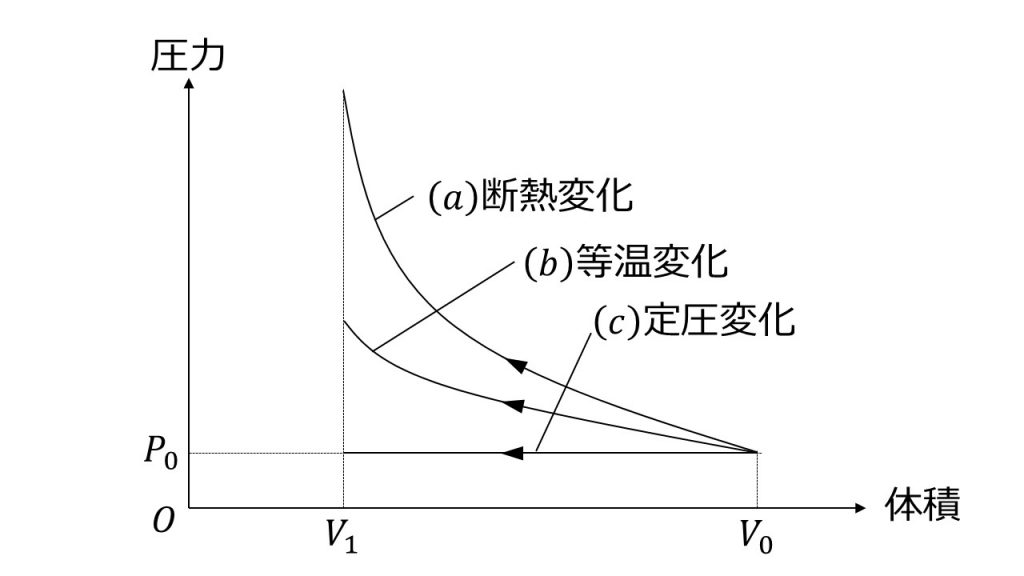
T T j i $ s9a s9 ¢ ä ¢ p C 図43 断熱過程,定積過程,等温過程からなる準静的なサイクル が成り立つ。過程ABは断熱膨張であるから,吸収する熱量はゼロである。一方, 外界にする仕事は,W ≃ p(T;V;n∆ V = nRT 1 V ∆V となる。ここでは理想気体の内部エネルギーの特徴について見ていきます。 1モルの理想気体に熱力学第一法則を適用します。 理想気体の仕事はその膨張/圧縮のみで決まるので、 また、内部エネルギーをt、vの関数として表し、その完全微分形をとります。等温 p と v −1 が比例 圧力 を下げると膨張する 断熱 p と v −5/3 が比例 1) 係数は気体の熱容量によって変わる。 単原子分子の場合 , 係数 。 二原子分子の場合 , 係数 。 圧力下げて膨張させて温度下げる 定圧 t と v が比例 温度を上げると膨張する




熱力学 11 等温変化 理系への道




高校物理 等温変化 Youtube
P0=10 気圧でn=10 mol の理想気体がある。この気体 が、T=300 K の温度を保ったまま、p1=1 気圧になるま で仕事しながら膨張した。仕事量と気体の吸熱量Q を求 めよ。 答 外界と系でやりとりした仕事をW (符号は外界から系へ の仕事を正)とすれば、dW = pdV である2 (等温膨張と仕事)1 モルの理想気体が温度300k で等温膨張し体積が2 倍になるとき、外界にする仕事w はいくらか? 3 (熱力学第一法則)熱力学第一法則は、系の状態変化において系が受け取る熱量∆q と仕事∆w との和がまた,理想気体の状態方程式より, =pv nrt 1 1 1 , =pv nrt 1 2 2 であるから,これを②に代入して整理すると, 1 0 2 1 = < nr w t t ( w1



3



P Vグラフとv Tグラフ 15年センター試験本試物理第5問 大学受験の王道
圧力100kPa 体積248dm^3 理想気体 単原子分子1mol の閉じた系を 248dm^3にする時の条件で幾つか指定されており 1 一定外圧10kPaで等温膨張 2 293Kで等温可逆膨張 とあり、1と2の条件下で気体が外界にした仕事と 1と2の条 理想気体が1×105乗Paの一定圧力の下、30Lから60Lに膨張した、このときの仕事wを求めよこの問題がわかりません↓解答を見ても、わかりずらくてお手上げです↓ 物理学 締切済 教え 等温体積変化における内部エネルギーの変化および熱の移動 理想気体の等温体積変化 理想気体の体積が v 1 から v 2 に変化したとき、系になされる仕事を w とする。 理想気体の状態方程式 pv = nrt を、p について解くと、p = nrt/v となる。
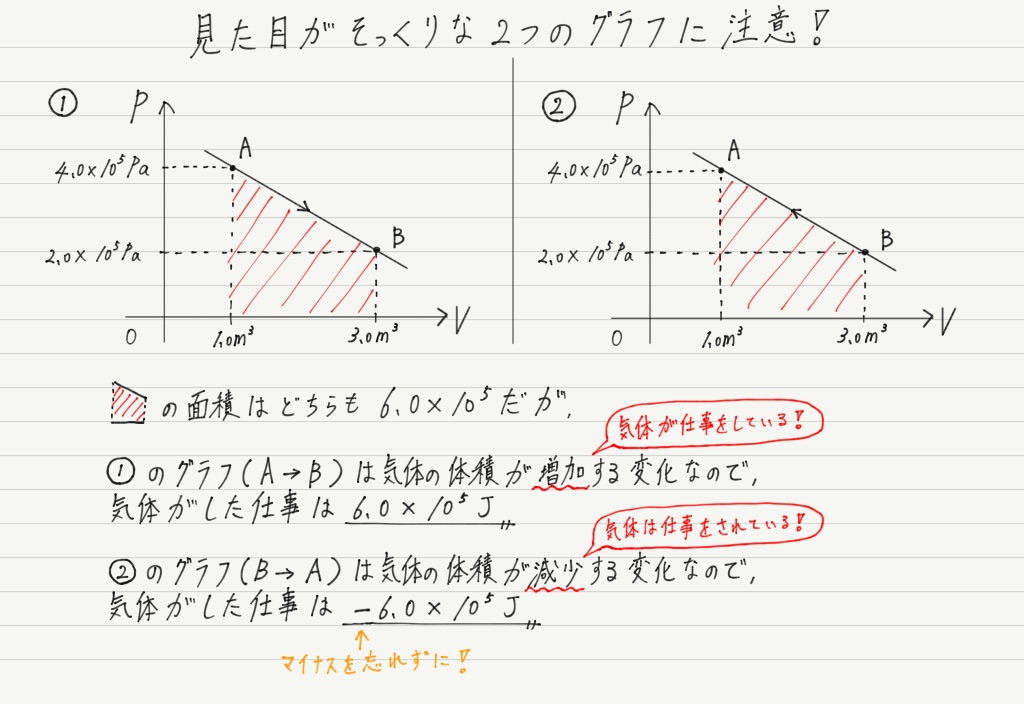



P Vグラフと気体のする仕事 高校物理をあきらめる前に 高校物理をあきらめる前に



Glanze Sakura Ne Jp
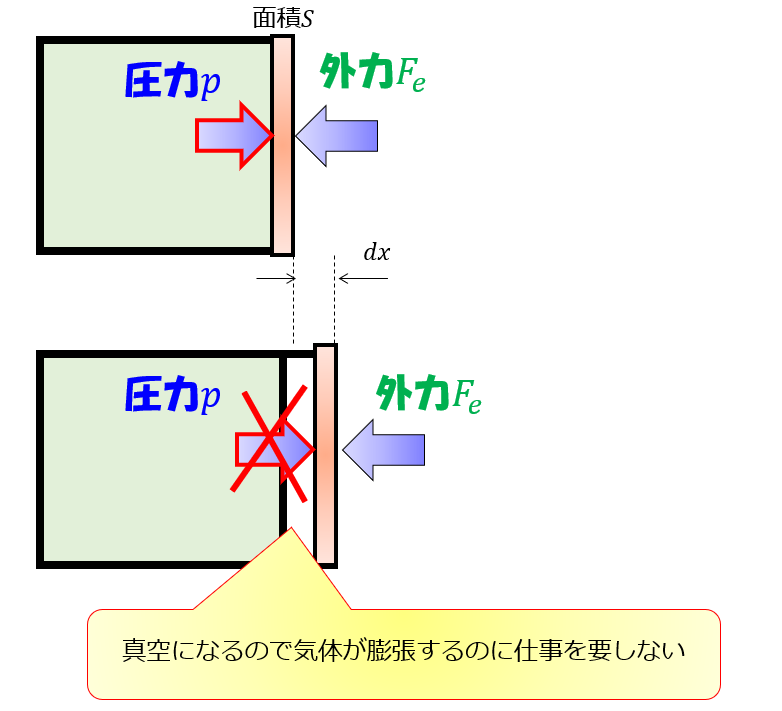
例)室温の1原子分子気体(理想気体)を断熱的に圧縮し て、体積が1/2になった時、温度は何度になるか? 断熱圧縮の式: 単原子気体の両比熱比γ:5/3 tを室温(300k)とし、圧縮後の温度をt'とすると 約0℃まで温度が上がる。理想気体の等温膨張の場合、 ( – ) は 0 となり、 の面積とは特に関係はありません。 これが定圧過程では意味を持ちます。 定圧過程では下の図のように、 (終状態のpv) – (初期状態のpv) = (膨張過程で系がする仕事 )になっていることがわかります。栓を抜いて気体が移動できるようになると、右のようにピストンが落ちた状態になる。 このとき理想気体の温度はどうなるだろう? 真空相手なら仕事はしないから、温度は変わらない。 断熱膨張しているんだから温度は下がる。




等温変化における仕事の求め方と圧力との関係 例題付き
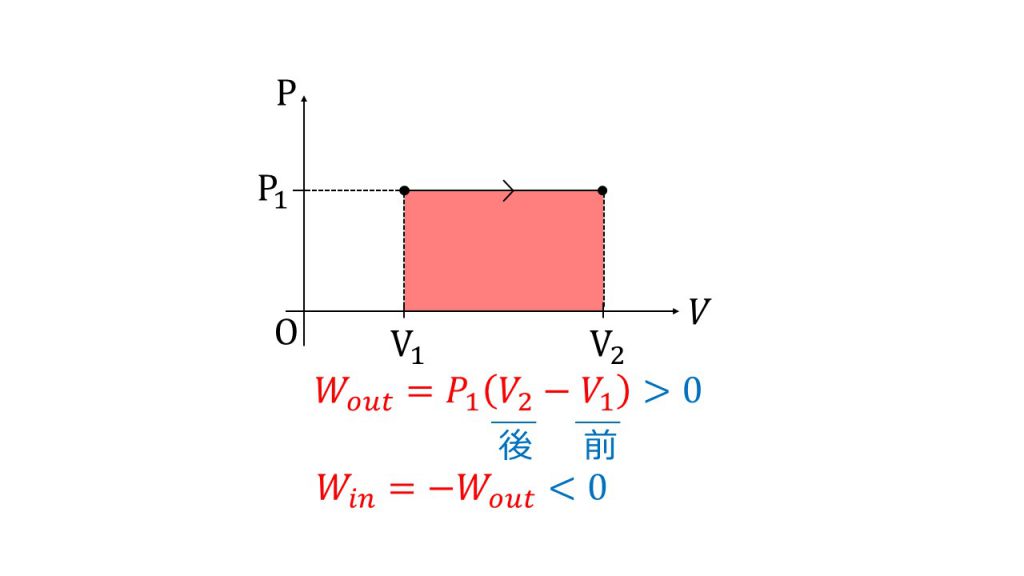



気体が外部にする仕事 Pdvになるわけ P Vグラフ 熱機関のサイクル 定積変化 定圧変化 等温変化 断熱変化 断熱自由膨張 大学受験の王道
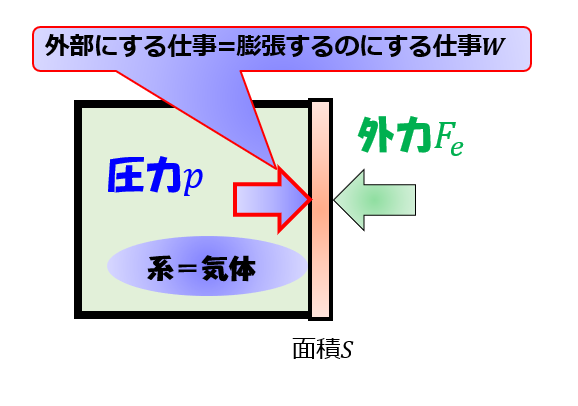
※理想気体で内部エネルギーが、 温度にしか依存しないことは下記の記事で示しています。 熱力学第一法則と理想気体を連立させる 熱力学第一法則 \(Q=\Delta U W\) ※\(W\)は気体が外部にする仕事 ↓ 断熱なので\(Q=0\) ↓ \(\Delta U=W\) 結論 等温過程では、気体の体積変化と仕事 • 気体が体積変化するときの仕事の大きさ • 気体が外からされた(自分が受けた)仕事 を正とする規約 • ΔV=(おわりのV)-(はじめのV) • 符号 圧縮:仕事をされた:δW>0,ΔV<0 膨張:仕事をした:δW<0,ΔV>0というような話をした。 熱力学では、この仕事とエネルギーの考え方を(熱力学で扱う状況に合わせて)変化させていかなくてはいけない そして、仕事以外のエネルギー移動の形態として「熱」というものを登場させていくことになる。 まず、等温変化における仕事について考えよう。
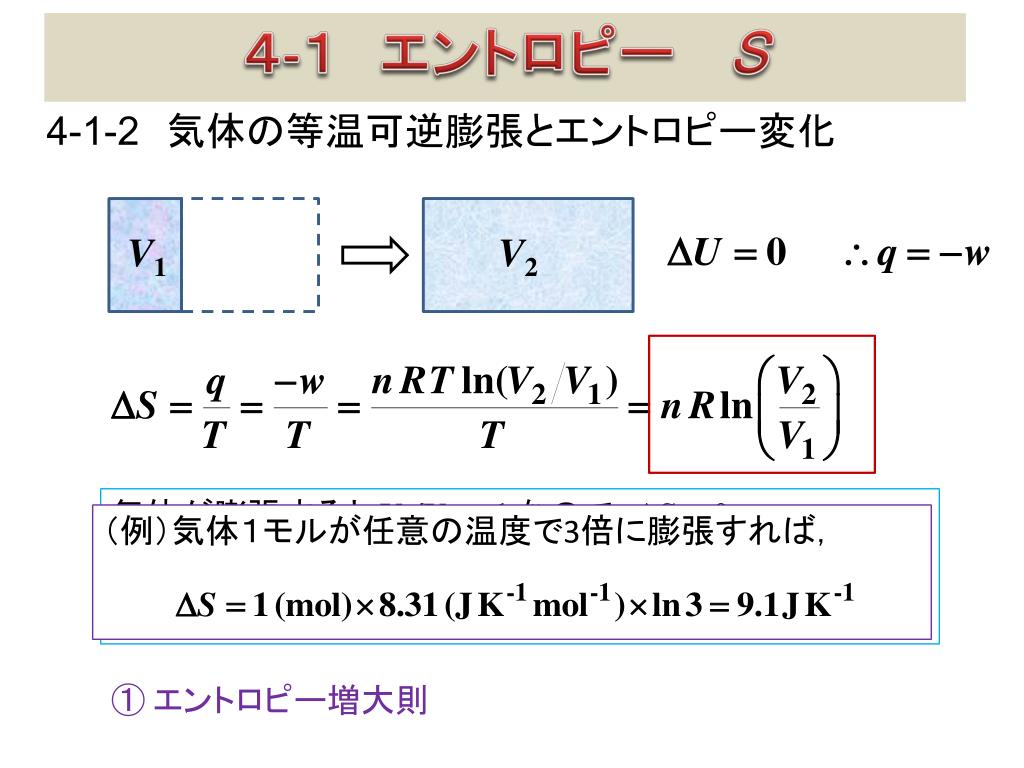



Ppt 物質の状態 I Powerpoint Presentation Free Download Id
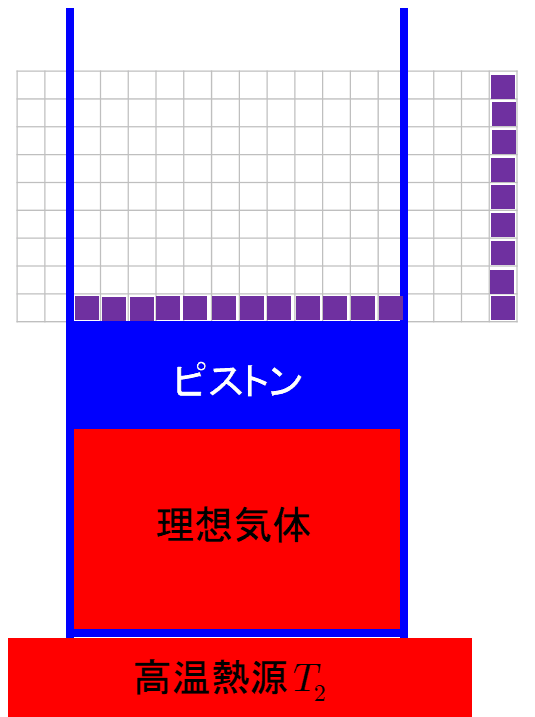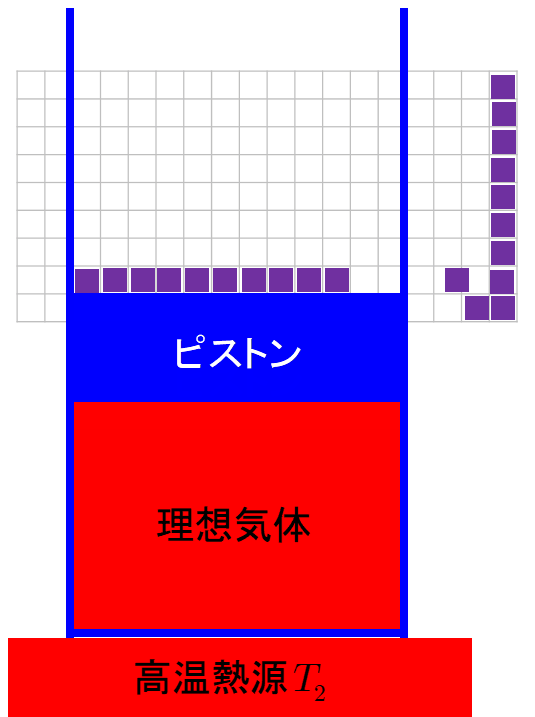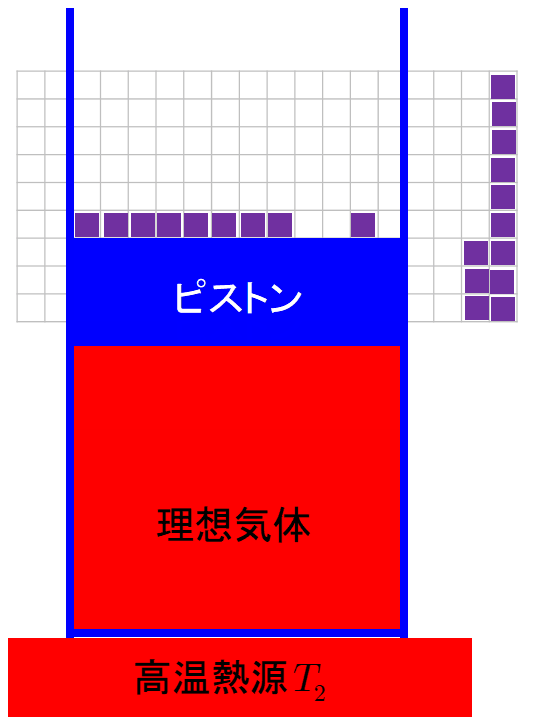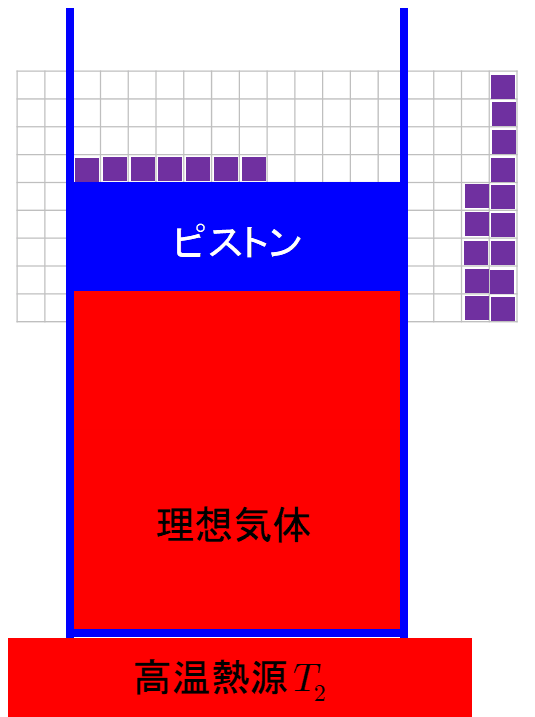



熱力学 まとめ 熱力学講義ノート
作業物質は理想気体なので、ぞれ ぞれの過程における、作業物質の 受ける熱と仕事は、 Ⅰ等温膨張 A(p 1,V 1,T 1)→B(p 2,V 2,T 1) Ⅱ断熱膨張 B(p 2,V 2,T 1)→C(p 3,V 3,T 2) Ⅲ等温圧縮 C(p 3,V 3,T 2)→D(p 4,V 4,T 2) ここで、Ⅰ・Ⅲは等温線、Ⅱ気体が負の仕事をする、というのは、気体が外力によって仕事をされる、外部から仕事を受ける、ということです。 但し、気体が断熱的に真空領域に向かって膨張 ( 自由膨張と言います ) する場合には、気体の 体積 が膨張していても、気体は外部に対して熱エネルギーを力学的エネルギー(外部へ仕事)に変える。 理想気体が熱を吸収、放出し、元の状態にもどる。 à 連続運転可能な機関 吸収した熱 qin = nrt a ln(v b /v a) 放出した熱 qout= nrt c ln(v d /v c) 断熱過程 t b v bγ1 = t c v c γ1 t a v a γ 1 = t d v d γ 等温過程 t




熱力学 11 等温変化 理系への道



理想気体と過程に関わる公式集
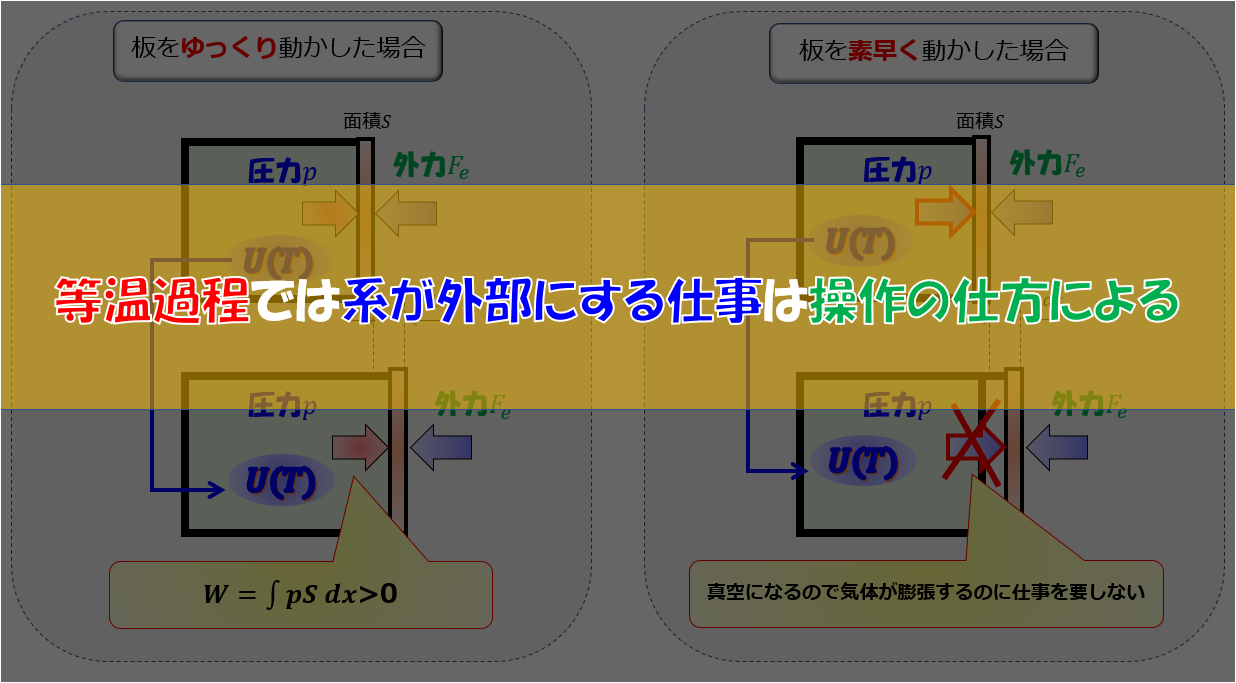
73 気体の断熱的体積変化 ・ 断熱的(adiabatic)な条件下で,理想気体 nmolの可逆膨張を考える 系と外界の間に熱の出入りがない 断熱変化の下での理想気体の可逆膨張 ・断熱変化では δQ =0 ⇒dU Q W= δδ (652)より,dU W=δ (731) 等温不可逆変化、外圧が一定の条件で仕事量を求める場合、 W=-P⊿Vでよろしいのでしょうか? それとも、モル数も考慮してW=-nP⊿Vとする必要があるのでしょうか? 等温可逆変化の場合はW=-nRTln(V2/V1)というように、nを掛ける公式が教科書に載っ 等温過程の場合に、操作の仕方によって系(気体)が外部にする仕事が変わります。 ↑こちらが本記事の趣旨です。 まずは状況説明をします。 今から2通りの操作の仕方を考えるのですが、初期状態はどちらも 「温度一定下にした状態で、気体n n molが



準静的操作 等温操作



P Vグラフ
理想気体の性質と状態変化(12) 等温変化と断熱変化の仕事量 理想気体の性質と状態変化(13) ポリトロープ変化 理想気体の性質と状態変化(14) 混合気体「一つの熱源の温度を下げることによって仕事をする以外に外界に 何の変化も残さずに周期的に働く機関は実現不可能である。」 注 周期性を要求しないのならば、例えば理想気体を断熱膨張させ れば全ての熱を仕事に変換できる。 42 Carnot サイクル



理想気体と過程に関わる公式集



熱力学第二法則




断熱過程 Wikipedia



1




等温変化の超解説 理系ラボ




熱力学 まとめ 熱力学講義ノート



P Vグラフ



気体の状態変化 わかりやすい高校物理の部屋



不可逆膨張の仕事 Shinshu Univ Physical Chemistry Lab Adsorption Group




熱力学 06 準静的過程 理系への道




5分でわかる ギブスの自由エネルギー エンタルピーやカルノーサイクルについて熱力学の視点から理系ライターがわかりやすく解説 ページ 3 3 Study Z ドラゴン桜と学ぶwebマガジン




なぜ 定圧過程のときだけ Q とエンタルピー変化 Dh が等しくなるのか Shinshu Univ Physical Chemistry Lab Adsorption Group
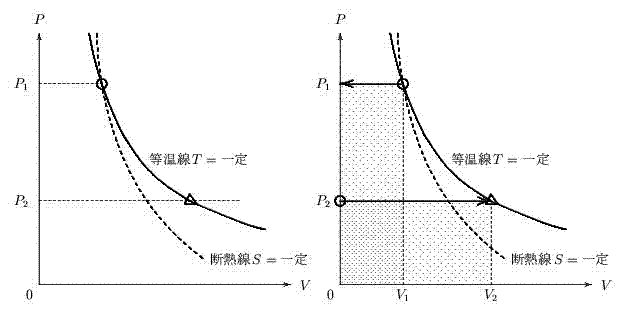



熱力学 00年問題 後期 01 1 26 京都大学ocw



熱機関の効率 ガス動力サイクル
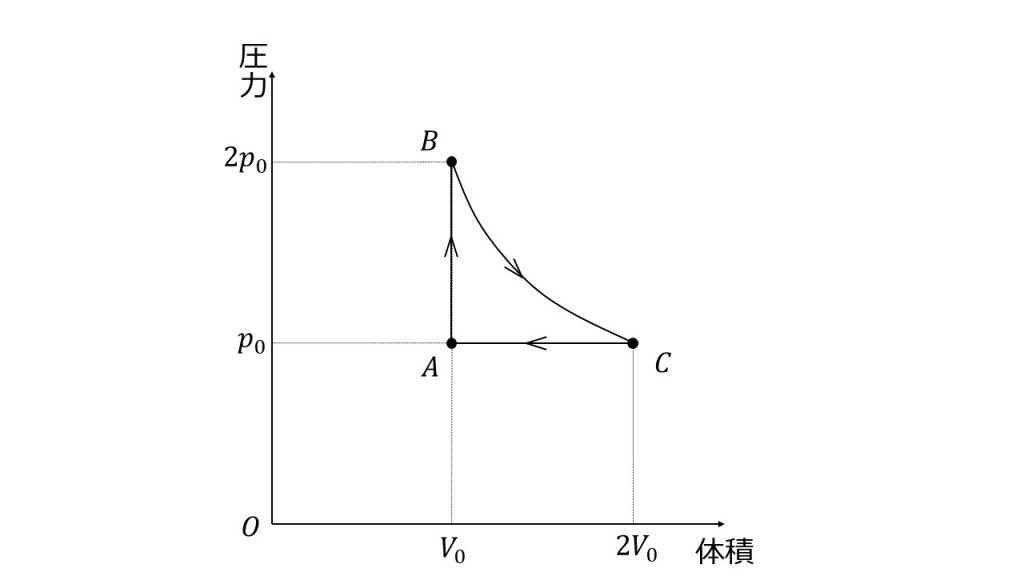



気体の状態変化 熱力学 問題演習 17年センター試験本試物理第3問b 大学受験の王道




断熱変化とp Vグラフ 高校物理の備忘録



気体の状態変化 わかりやすい高校物理の部屋




高校物理 断熱変化 ポアソンの法則 練習編 映像授業のtry It トライイット
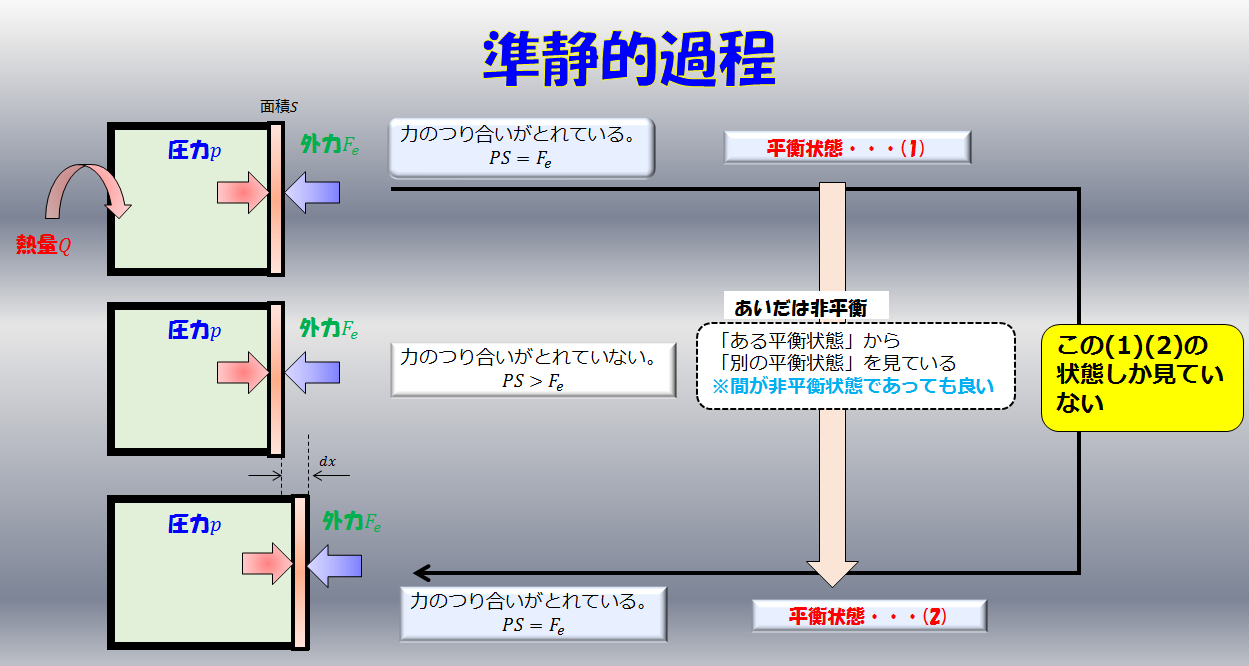



等温過程では系が外部にする仕事は操作の仕方による 宇宙に入ったカマキリ



3




熱力学解説送ってくれると嬉しいです Clearnote




等温変化の超解説 理系ラボ
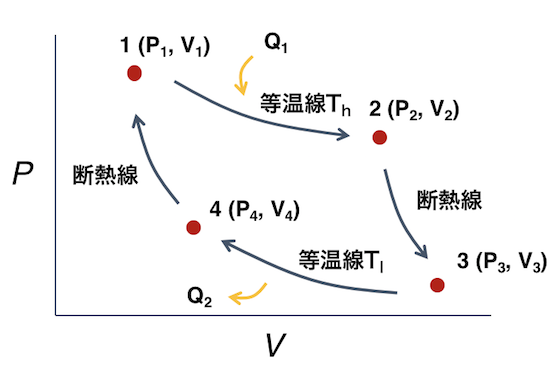



カルノーサイクル 温度thとtlで等温膨張 圧縮を行い その間を断熱膨張 圧縮で結ぶ一連のサイクル



5 2 熱力学第一法則 スペクトル色々




等温 定圧 定積変化とp Vグラフ 高校物理の備忘録



後藤信行 Jp
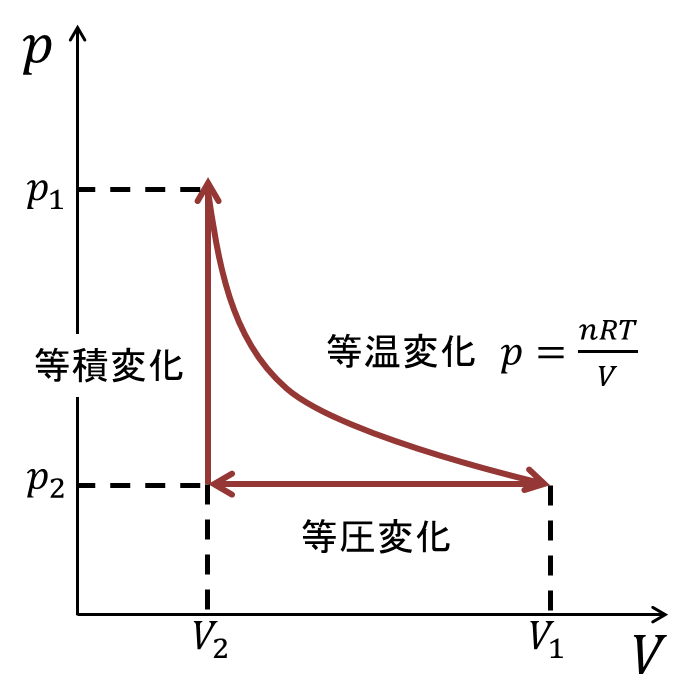



物理とか 理想気体の熱機関




高校物理 気体が外部にした仕事 映像授業のtry It トライイット



Www1 Doshisha Ac Jp




高校物理 気体の熱サイクルと熱効率 受験の月




熱と波動 総合システム 後期水曜日3時限 金曜日2時限 担当教員 鎌田 裕之 総合システム工学科 1年次後期 選択必修 4単位 熱 波動分野は工学の自然科学的な基礎であり その方法と考え方を身につけることは必要不可欠である 1回から1




熱と波動 総合システム 後期水曜日3時限 金曜日2時限 担当教員 鎌田 裕之 総合システム工学科 1年次後期 選択必修 4単位 熱 波動分野は工学の自然科学的な基礎であり その方法と考え方を身につけることは必要不可欠である 1回から1




4つの物理過程について Shinshu Univ Physical Chemistry Lab Adsorption Group




高校物理 熱力学第一法則 気体の定積モル比熱cvと定圧モル比熱cp 熱機関と熱効率e 受験の月




断熱変化とポアソンの法則 導出 理系ラボ
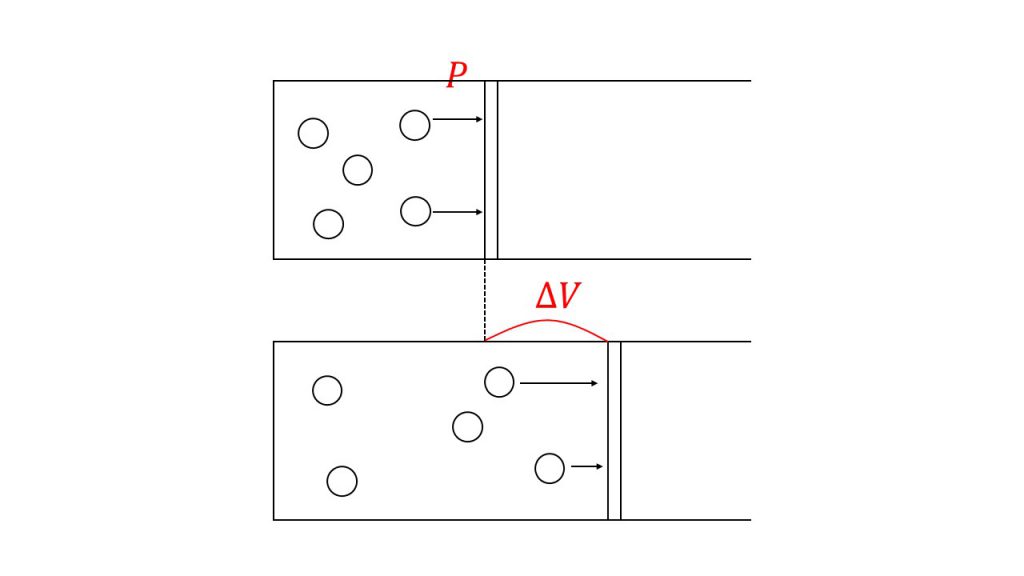



気体が外部にする仕事 Pdvになるわけ P Vグラフ 熱機関のサイクル 定積変化 定圧変化 等温変化 断熱変化 断熱自由膨張 大学受験の王道



熱力学15年度第10講
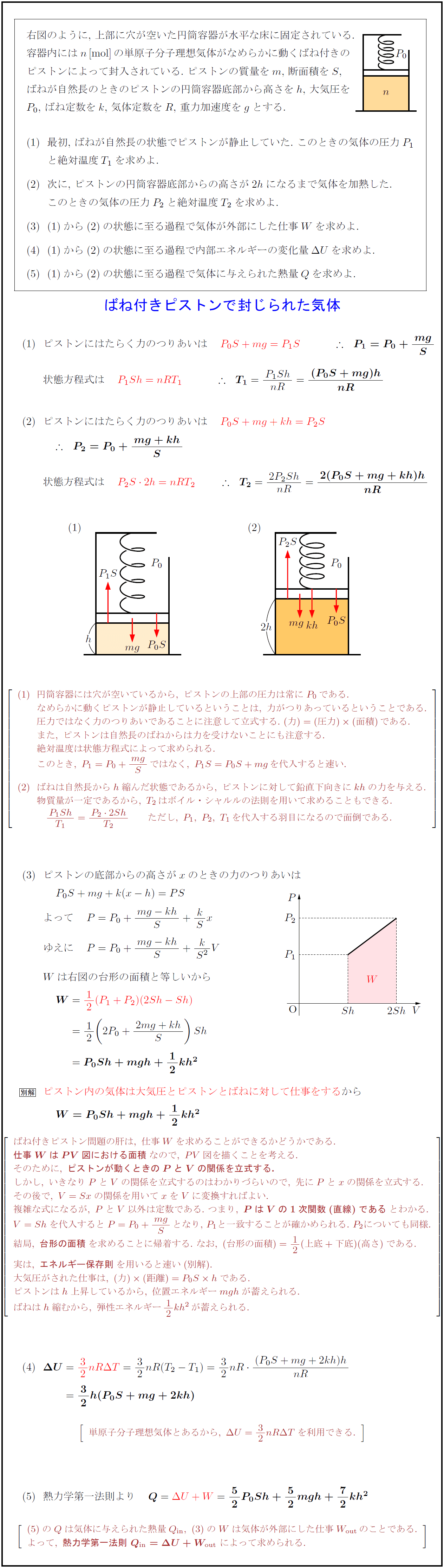



高校物理 ばね付きピストンで封じられた気体 受験の月



断熱可逆膨張の問題についてです 答えがなく困っています よろ Yahoo 知恵袋



5 2 熱力学第一法則 スペクトル色々
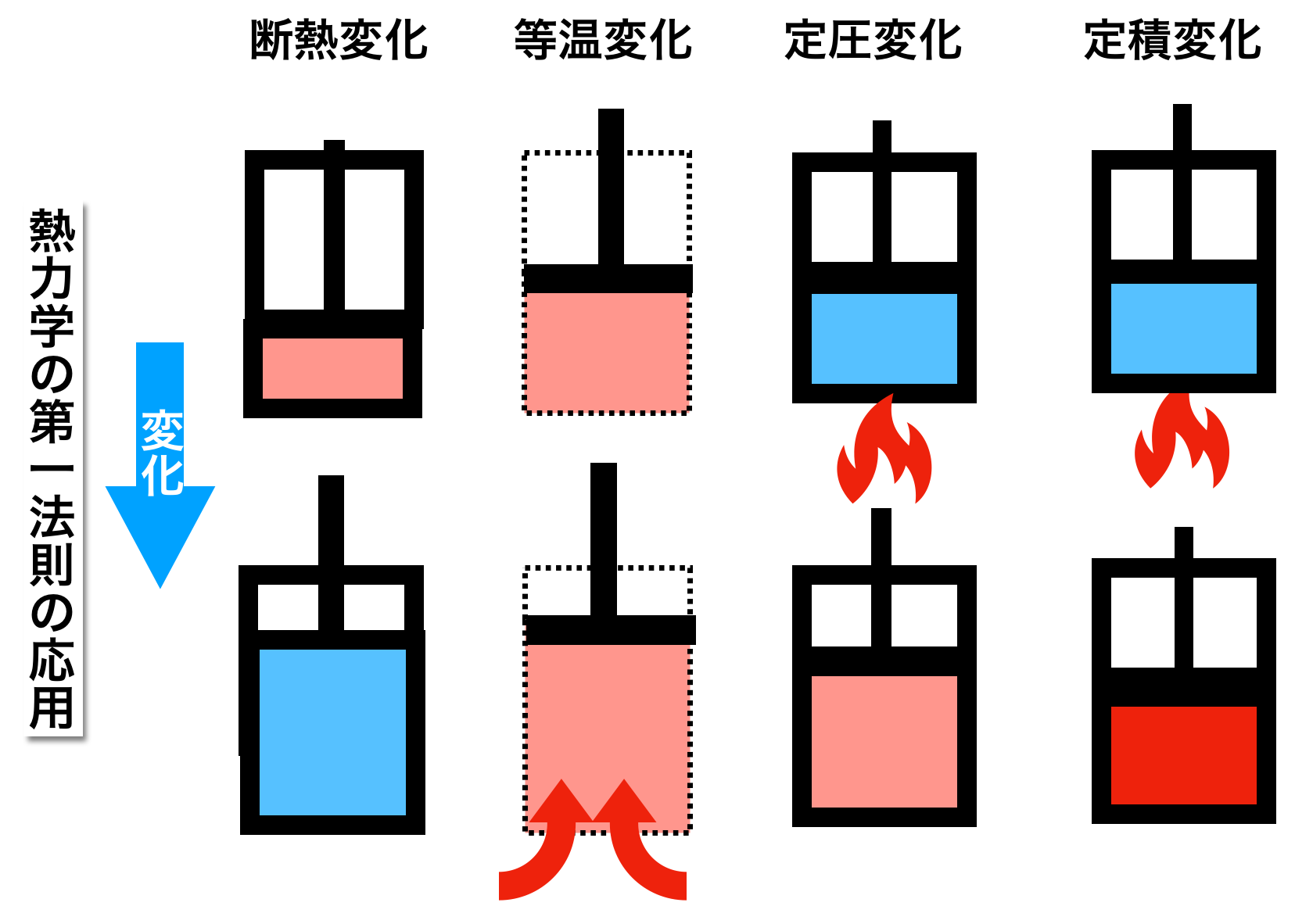



断熱変化と等温変化 熱力学の第一法則2 色と形で気象予報士




この3問あってますか Clearnote



5 6 断熱変化 スペクトル色々



理想気体の性質と状態変化 数学活用大事典



ときわ台学 化学熱力学 混合エントロピー 化学ポテンシャル
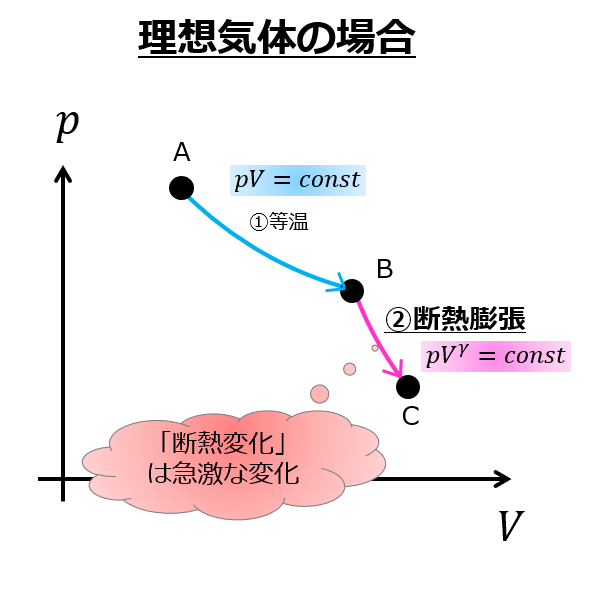



熱力学 カルノーサイクルから最大効率の熱機関を学ぼう 宇宙に入ったカマキリ
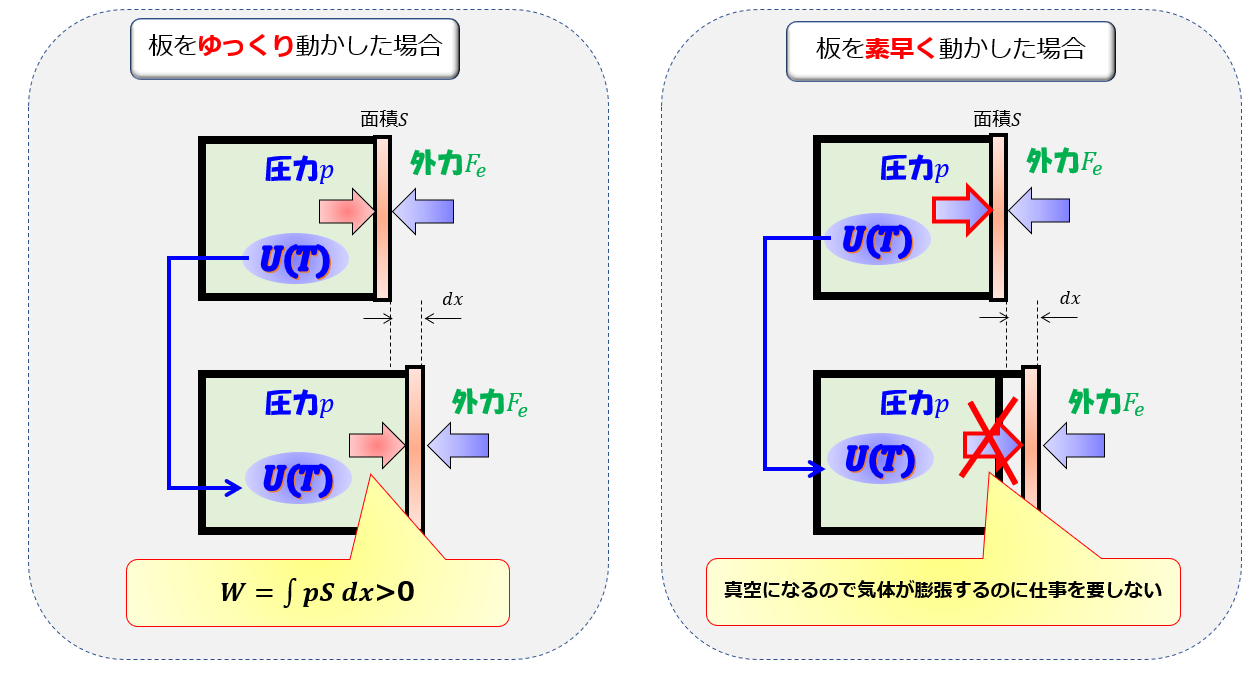



等温過程では系が外部にする仕事は操作の仕方による 宇宙に入ったカマキリ



5 2 熱力学第一法則 スペクトル色々




気体が膨張すると温度は下がるのか それとも温度は上がるのか 宇宙に入ったカマキリ
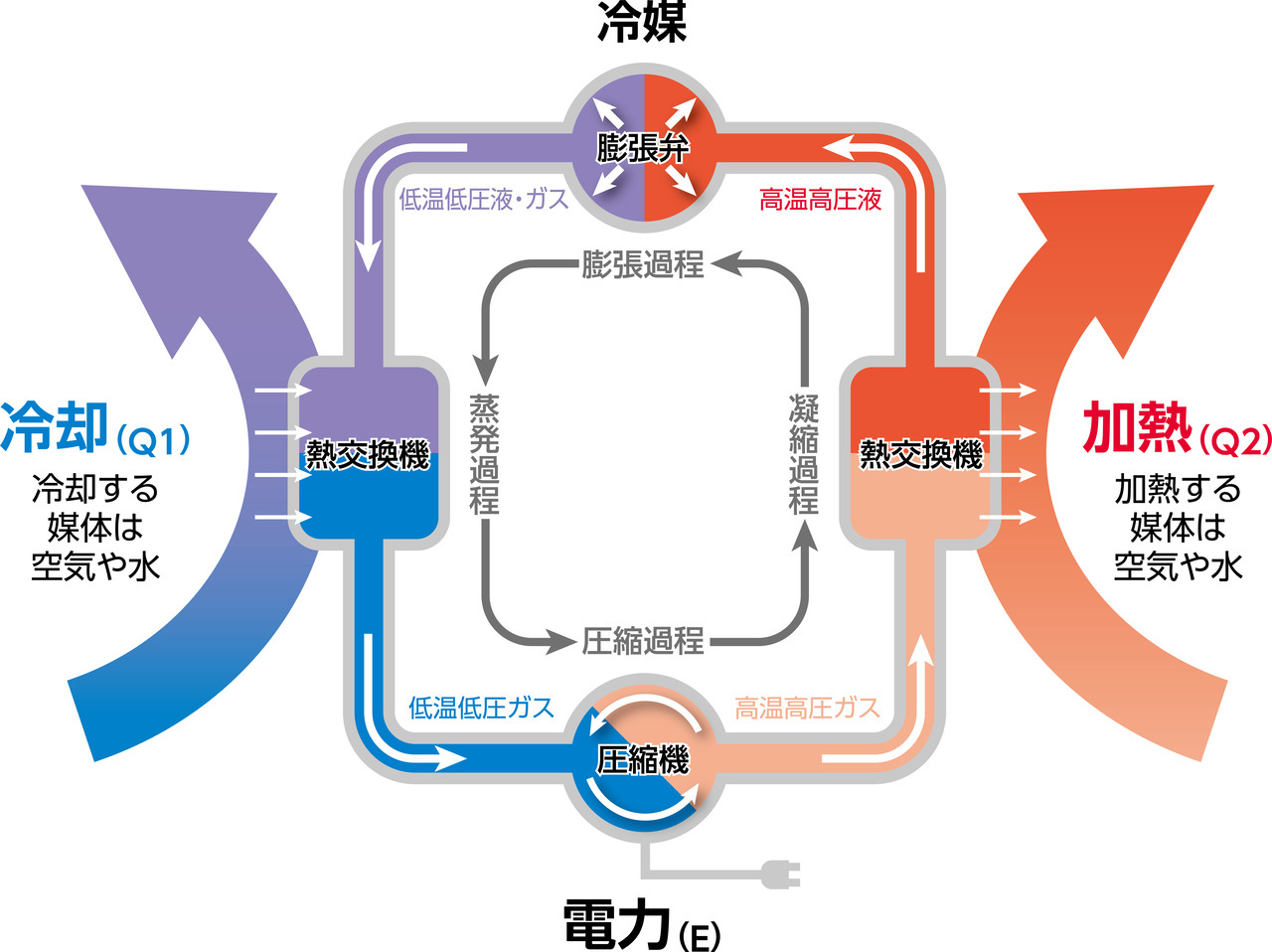



ヒートポンプの謎 黒豆納豆の特許翻訳



P Vグラフ




19 7 多段階の圧縮過程の W ページ 2 Shinshu Univ Physical Chemistry Lab Adsorption Group



Lasti U Hyogo Ac Jp



カルノーサイクル入門 理想気体のカルノー効率について ある社会人の勉強記録



エントロピーとは 10 カルノー サイクルについて 炉端での話題




スターリングサイクル



Kz Tsukuba Ac Jp




P Vグラフとv Tグラフ 15年センター試験本試物理第5問 大学受験の王道




B Cのところがよく分かりません 物理の熱力学の分野なんですが B Cは等温 Clearnote



気体のモル比熱




19 7 多段階の圧縮過程の W ページ 2 Shinshu Univ Physical Chemistry Lab Adsorption Group




19 3 実在気体と仕事 ページ 2 Shinshu Univ Physical Chemistry Lab Adsorption Group




Ppt Cbt 基礎薬学特別講義 I Powerpoint Presentation Free Download Id




等温 定圧 定積変化とp Vグラフ 高校物理の備忘録



エントロピーとは コトバンク



等温過程では系が外部にする仕事は操作の仕方による 宇宙に入ったカマキリ



Adoko 熱力学 気体の熱力学



Hep1 C U Tokyo Ac Jp




問6 問7がどうやってといたらいいかわからないです 解答が無いので答えも知り Clearnote




断熱変化とポアソンの法則 導出 理系ラボ
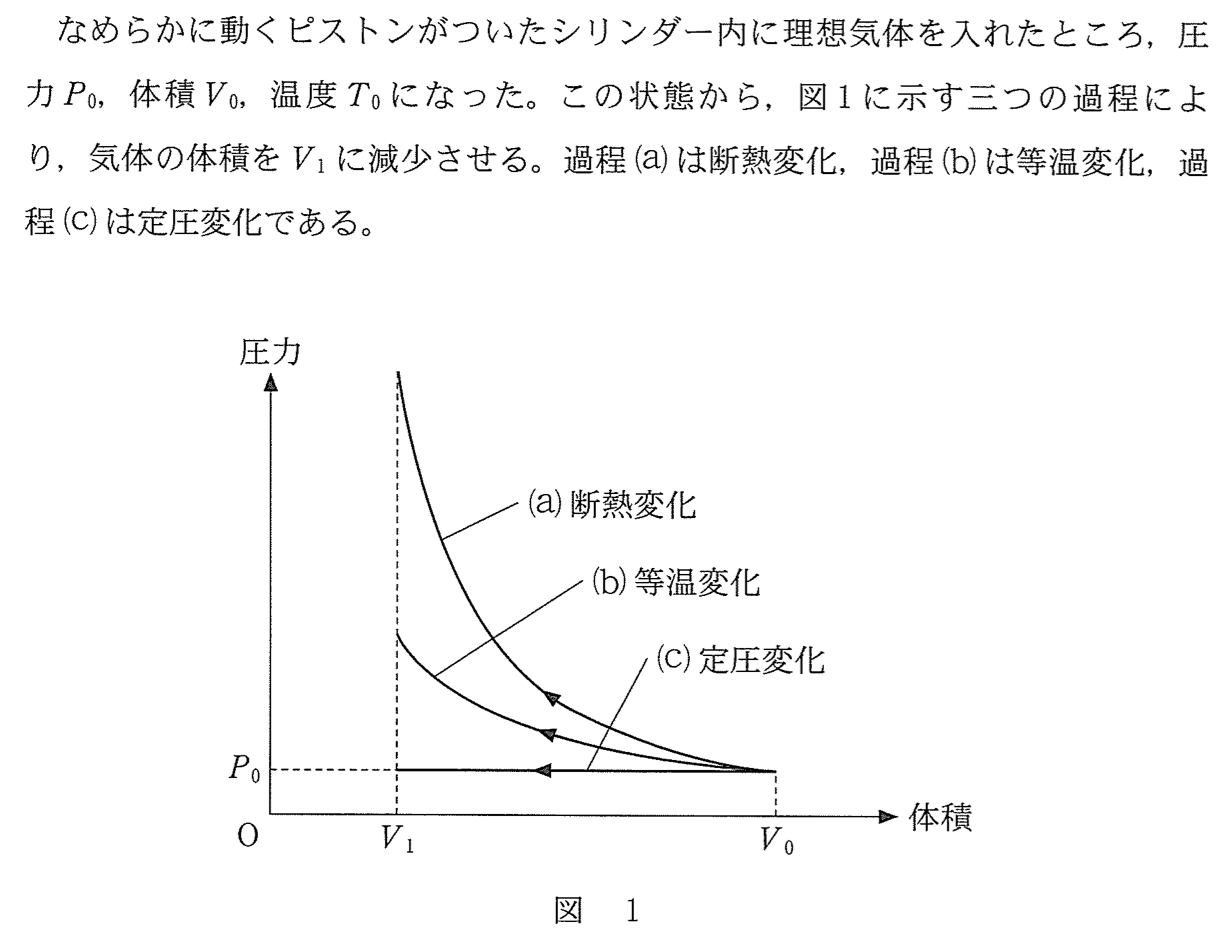



センター15物理第5問 断熱 等温 定圧変化 理科が好き Com
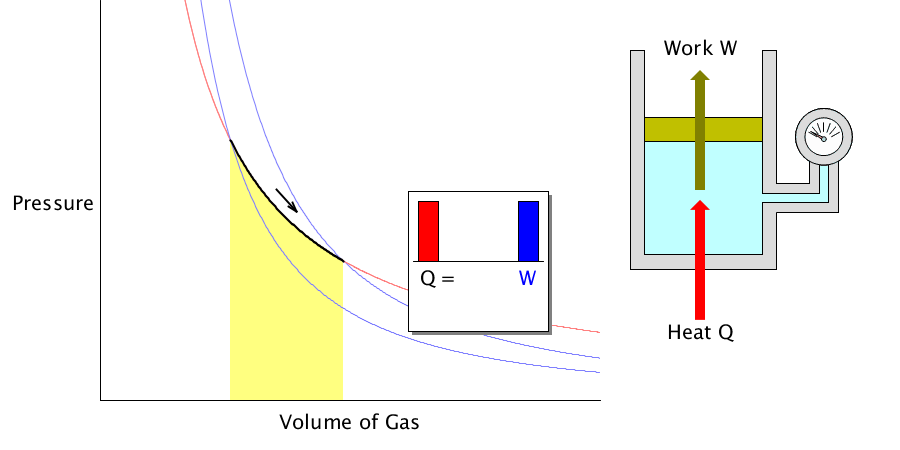



Pv図 Java実験室



気体の状態変化 わかりやすい高校物理の部屋



カルノーサイクルの仕事と熱効率



断熱変化と等温変化の仕事理想気体は等温圧縮より 断熱圧縮の方が所要仕 Yahoo 知恵袋



等温過程では系が外部にする仕事は操作の仕方による 宇宙に入ったカマキリ
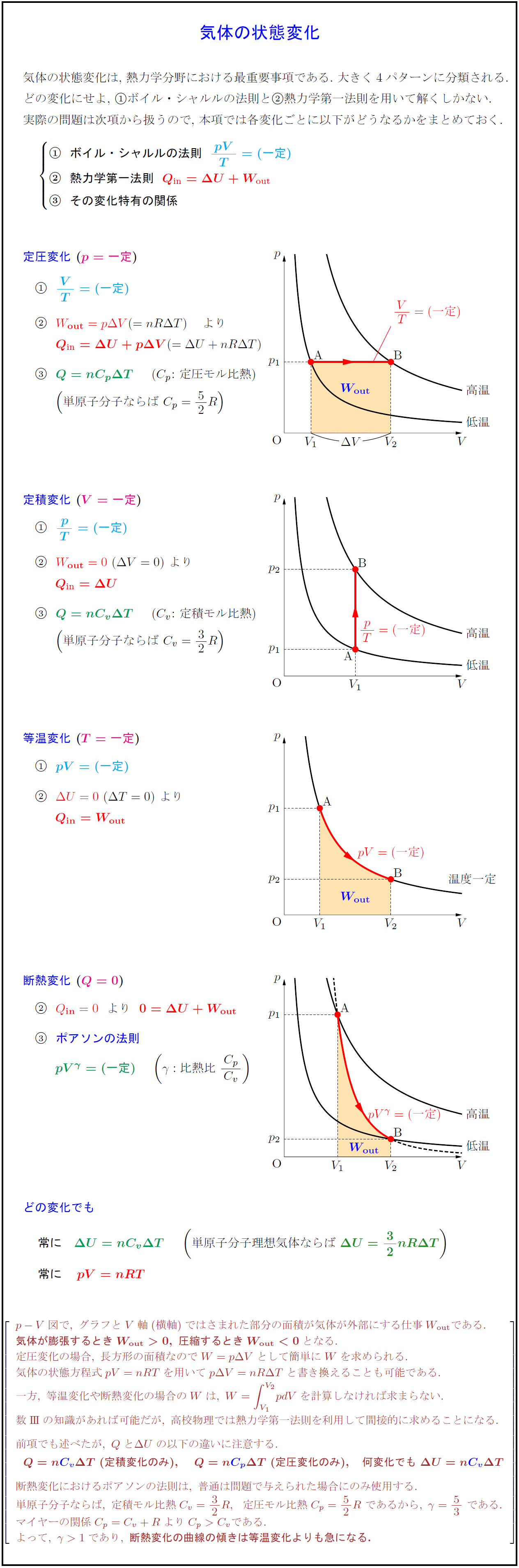



高校物理 気体の状態変化 定圧変化 定積変化 等温変化 断熱変化 受験の月



後藤信行 Jp



Adoko 熱力学 気体の熱力学




等温過程 Wikipedia




高校物理 断熱自由膨張と気体の混合 受験の月




等温 定圧 定積変化とp Vグラフ 高校物理の備忘録



等温過程では系が外部にする仕事は操作の仕方による 宇宙に入ったカマキリ



一定量の単原子分子理想気体の状態を 次のp V図のように A B Yahoo 知恵袋

No comments: